This Math video lesson is designed for 6-12 years old children to help them understand the concept of prime numbers and prime factorization using Montessori pegs and board.
What are prime numbers with examples?
Prime numbers are natural numbers greater than 1 that can only be divided by 1 and themselves. For example, 7 is a prime number. It can only be made by multiplying 7 by 1. In other words, a prime number is a number that can only be divided evenly by itself and 1.
List of Prime Numbers
Some of the prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, and so on.
What is Prime Factorization?
It is the process of finding the prime factors of a given number, which are the prime numbers that divide the given number exactly without leaving any remainder. It is the way to write a number as the product of prime numbers.
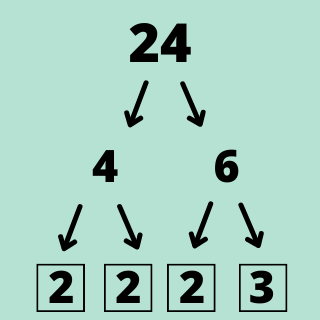
For example, let’s consider the number 24. The prime factors of 24 are 2, 2, 2, and 3. Notice that 2 is a prime number and 3 is also a prime number. Moreover, 2x2x2x3 = 24. This implies that every positive integer greater than 1 can be expressed as a product of prime factors in a unique way, up to the order of the factors.
Methods of Prime Factorization
There are 3 methods of Prime factorization for 6 -12-year-olds
- Trial division method
- Factor Tree Method
Trial Division Method
One of the most common methods for finding the prime factors of a number is the trial division method. In this method, we divide the given number by the smallest prime number, which is 2, and keep dividing until we get a quotient that is no longer divisible by 2. Then we move to the next smallest prime number, which is 3, and keep dividing until we get a quotient that is no longer divisible by 3. We continue this process until we cannot divide by any prime number greater than 1.
Let us understand the concept of Prime factorization using a tabular form. For example, finding prime factors of 144
| Steps | Prime Factors | Result |
| Step1: Divide 144 by 2 | 2 | 72 |
| Step2: Divide 72 by 2 | 2 | 36 |
| Step3: Divide 36 by 2 | 2 | 18 |
| Step 4: Divide 18 by 2 | 2 | 9 |
| Step 5: Divide 9 by the next prime number 3 | 3 | 3 |
| Step 6: Divide 3 by 3 | 3 | 1 |
Therefore, the prime factors of 144 are 2x2x2x2x3x3 or 24x32
Factor Tree method
Prime factorization by factor tree method is a way to find the prime factors of a number by creating a tree of its factors and simplifying it until all factors are prime. It is a visual method that is often used in math classes to teach students how to factor numbers. To use the factor tree method, you first write the number you want to factor at the top of the tree. Then, you find two factors of the number and write them below it, connected by a line. You keep finding the factors of each number until all the factors are prime numbers. Once every factor is prime, you write them all along the bottom of the tree. The factor tree method is a great way to get a visual representation of the prime factors of a number. It is especially helpful for larger numbers that may be difficult to factor in using other methods. Students often find this method more engaging and easier to understand than other methods because it is a visual representation.
Prime Factorization in Montessori
Prime Factorization in Montessori education is introduced using pegs and boards
Materials Required
- Pegboard,
- Box of hierarchically colored pegs
- Tickets or mathematical alphabet and signs
- Squared paper
Prerequisites
- A child must be introduced to multiples and multiple factors.
- A child must be familiarized with prime numbers
- A child must be familiar with math material: pegs and boards.
How Prime Factorization is Introduced to the Child?
Now keeping the trial division method in mind follow the below steps:
- Invite the child to the table with the Montessori math material, pegs, and board.
- Place the board in front of the child and tell them, today we understand the concept of prime factors and find out the prime factors of a number.
- For example, let us find the prime factors of the number 12. First, place the number 12 using pegs (one blue peg representing tens and eight green pegs representing units) on the board.
- Now place a division line and then place the number 2 ticket on the right side of it.
- Ask the child to divide the number 12 by 2, the answer comes to 6. Now, add 9 pegs below 12.
- Again, ask the child to divide the result of step 5 by 2. The answer will be 6/2= 3. Now add 3 pegs below 6.
- Ask the child to divide 3 by 2. The child cannot divide further. Thus, ask the child to try dividing no. 3 by the next possible prime number i.e. 3.
- The 3 is completely divided by 3 and remains no remainder.
- As shown in the video, ask the child to write the quotient numbers in an expression i.e. 2x2x3, and tell them 2x2x3 are prime factors of the number 12.
- Invite the child to try finding prime factors of other numbers such as 36 and 144.
Applications of Prime Factorization
The prime factorization has a wide range of applications in various fields.
- In number theory, prime factorization is used to study the properties of prime numbers, such as the distribution of prime numbers among the integers.
- Cryptography relies heavily on prime factorization, as it is used to create secure encryption algorithms. For example, the RSA encryption algorithm is based on the difficulty of factoring large composite numbers into their prime factors.
- In computer science, prime factorization is used in various algorithms, such as Pollard’s rho algorithm and the quadratic sieve algorithm, for integer factorization. These algorithms are used to find the prime factors of large integers, which is a computationally difficult problem.
- HCF (Highest Common Factor) and LCM (Least Common Multiple) are mathematical concepts used in finding the largest common factor and smallest common multiple of two or more numbers that rely heavily on the concept of prime factorization.
Allow the child to explore this practical method for an easy understanding of the prime factors and how to find prime factors of a number.
Related Video Resources
- Addition and subtraction of squares and cubes
- Notation of squares
- Notation of cubes
- How to find factors of a number
To watch more math video resources, click here.
Video Created by: Justine McNeilly
FAQs
- How do you find prime factors?
The simplest way to find prime factors of a number is the division method. To find the prime factors of a number, you need to factorize the number into its prime factors. This can be done by dividing the number by its smallest prime factor, then dividing the result by its smallest prime factor, and so on until the result is a prime number. The prime factors of the original number are all the prime numbers that were used as divisors in this process.
- What is prime factorization?
Prime factorization is identifying the prime numbers that divide a given number exactly, without leaving any remainder. It is the way to write a number as the product of prime numbers.
- What are the first 7 prime numbers?
The first 7 prime numbers are 2, 3, 5, 7, 11, 13, 17.
- What are the two different methods to find the prime factors of a number?
The two different methods to find the prime factors of a number are 1) the Factor Tree Method and 2) Division Method.
- What is the difference between prime numbers and prime factors?
Prime numbers are numbers that are only divisible by 1 and themselves, such as 2, 3, 5, 7, 11, and so on. Prime factors are prime numbers that can be multiplied together to get a particular number. For example, the factors of 36 are 2, 2, 3, and 3, and the prime factors of 36 are 2 and 3.
Tags
- elementary level
- Math





